고정 헤더 영역
상세 컨텐츠
본문
고전제어 2부
고전제어 1부... 현대제어와의 차이제어기 설계에 필요한 제어 이론에는 고전제어와 현대제어가 있다. 고전제어에서는 시스템을 단일 입력과 단일 출력의 전달함수로 나타낸다.그리고 영점과
zin9.tistory.com
고전제어에 이어 현대제어를 간단히 알아보자.
그 전에 명심해야 할 것은, 모터제어기설계에 있어 고전제어 또는 현대제어만 하는 것이 아니다.
고전제어와 현대제어를 적절히 섞어 사용하여 최적의 제어기를 설계하는 것이 목적이다.
현대제어에서는 상태 변수로 시스템의 방정식을 세운다.
즉, 변수가 1개 이상인 상태 변수를 사용한다.
위치, 속도, 부하토크로 이루어진 상태 변수를 사용하여 상태 관측기를 설계할 것이다.
책에서는 "전차원 관측기"를 소개하는데, 그 의미를 설명하지 않고 있다.
"전차원 관측기"는 모든 상태변수를 추정하는 관측기를 의미한다.
1. 전차원 관측기(Full Order Observer)
들어가기에 앞서 기호에 대한 설명을 한다.
상태 변수 벡터인 x에 대해서 가운데 문자의 모자는 추정치를 의미하고, 오른쪽의 물결무늬는 추정된 상태의 오차를 나타낸다.

일반적으로 시스템은 아래와 같이 표현한다.
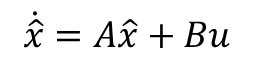
A는 시스템의 행렬, B는 입력 행렬, u는 시스템의 입력이다.
u는 이 시스템의 제어 입력으로, 속도제어기의 출력(=토크 지령)이다.
상태 변수 벡터 x의 초기값 x(0)를 알고 있으면, 추정치의 초기값을 x(0)로 설정함으로써 만족스러운 관측기를 구성할 수 있다.
관측기가 동작하기 전에 추정치의 초기값을 x(0)으로 하는 편이 좋다.
오차의 동적 방정식은 아래와 같으며, 행렬 A의 고유값의 절대값이 작은 경우에 수렴 속도가 매우 낮아지게 된다.
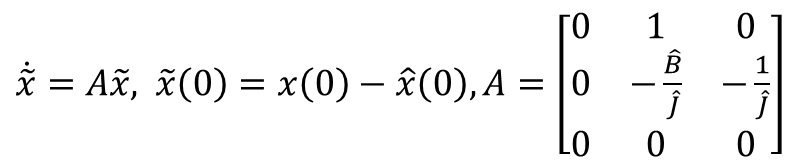
※ 고유값 풀어보기
A가 어떻게 나오는지는 나중에 설명하고, A의 고유값의 절대값이 작아지려면 J가 크거나 B가 작아야 한다.
점성마찰계수 B는 예측이 다소 어렵기 때문에, 관성모멘트 J가 크면 수렴 속도가 낮아진다.
관성모멘트가 크다는 것은 관성이 크다는 것이므로, 응답이 느려질 것이므로 수렴 속도가 낮아질 것이다.
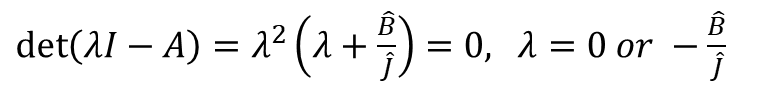
2. 루엔버거 관측기(Luenberger Observer)
이 관측기는 전차원 관측기의 한 종류로, 추정된 상태와 측정된 상태의 오차를 궤환하여 상태 추정 모델을 연속적으로 수정해 나가는 관측기이다.
설명하기 전에 상태 방정식을 정리한다.
변수에 모자가 있는 이유는 상태 관측기를 통해 추정해야 한다는 의미이다.
J와 B 또한 기계 시스템의 값을 추정해서 입력해줘야 하므로 기호에 모자가 붙어있다.
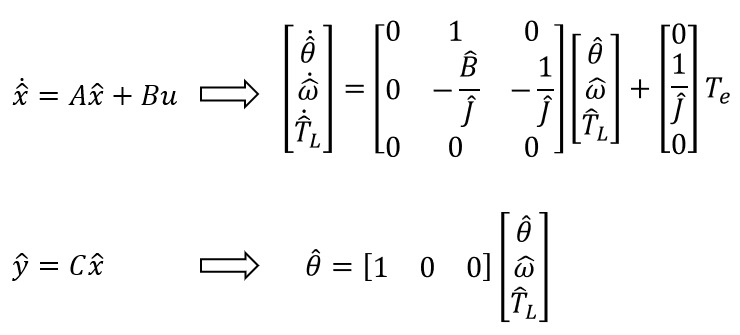
루엔버거관측기의 수식과 그림은 다음과 같다.
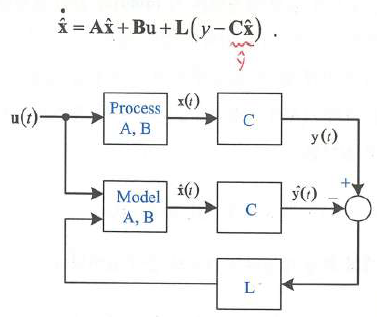
L은 비례 게인으로 만족스러운 추정 오차 특성을 얻기 위해 설계자가 설정하는 값이다.
그림 1으로부터 오차에 대한 상태 방정식을 구하면 다음과 같다.
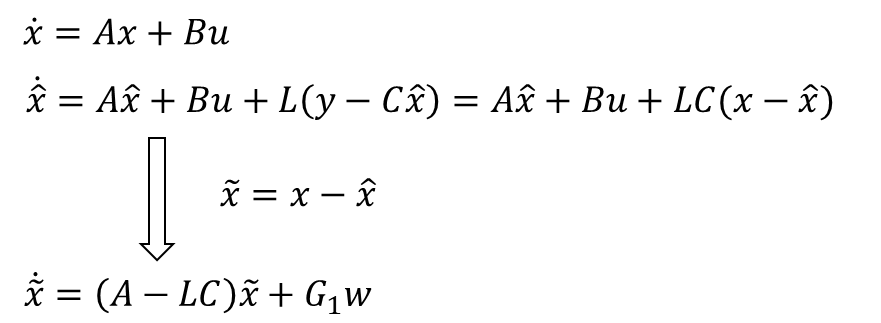
여기서 G1은 외란이 상태 변수 추정에 미치는 영향을 나타낸 행렬이고, w는 시스템의 외란을 나타낸 행렬이다.
외란이 있더라도 오차를 허용할 만큼 작게 하게 위해선, 아래의 특성방정식의 해를 구하여 비례 게인 L의 값을 정하면 된다.
특성방정식은 3차 함수로 나타나며, 총 3개의 해가 나온다.
계수를 비교하여 비례 게인 L의 값을 구할 수 있다.
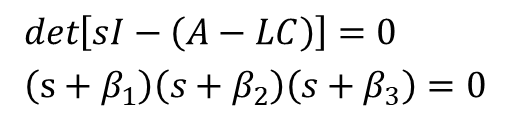
2부에서는 비례 게인 L의 계산, 전차원 관측기의 물리적 이해, 외란 관측기에 대해 알아본다.
출처: 전기기기제어론 4.3.3 상태 관측기를 이용한 속도의 추정
'제어이론' 카테고리의 다른 글
| 현대제어 2부 - 속도 관측기 설계 (2) | 2024.06.16 |
|---|---|
| 고전제어 1부... 현대제어와의 차이 (0) | 2024.06.09 |
| 약계자 제어(Field Weekening Control) - 1부 (3) | 2024.03.30 |
| PWM 이해하기 - 2부 (5) | 2024.02.19 |
| PWM 이해하기 (2) | 2024.01.29 |




