고전제어 2부

고전제어 1부... 현대제어와의 차이

 

이번 시간에는 MATLAB/Simulink로 PI게인에 따른 근궤적의 변화를 알아보고자 한다.

그림 1을 보면 빨간 원 안에 조그만 화살표를 볼 수 있다.

이는 각 블록을 잇는 선을 선택하고 우클릭하여 [선형분석점]을 누르면, [개루프 입력] 또는 [출력 측정]을 선택하면 된다.

Simulink 옵션에 따라 없을 수도 있다.

<그림 1. 위치-속도 제어 시스템>

 

<시뮬레이션 파라미터>

 

 

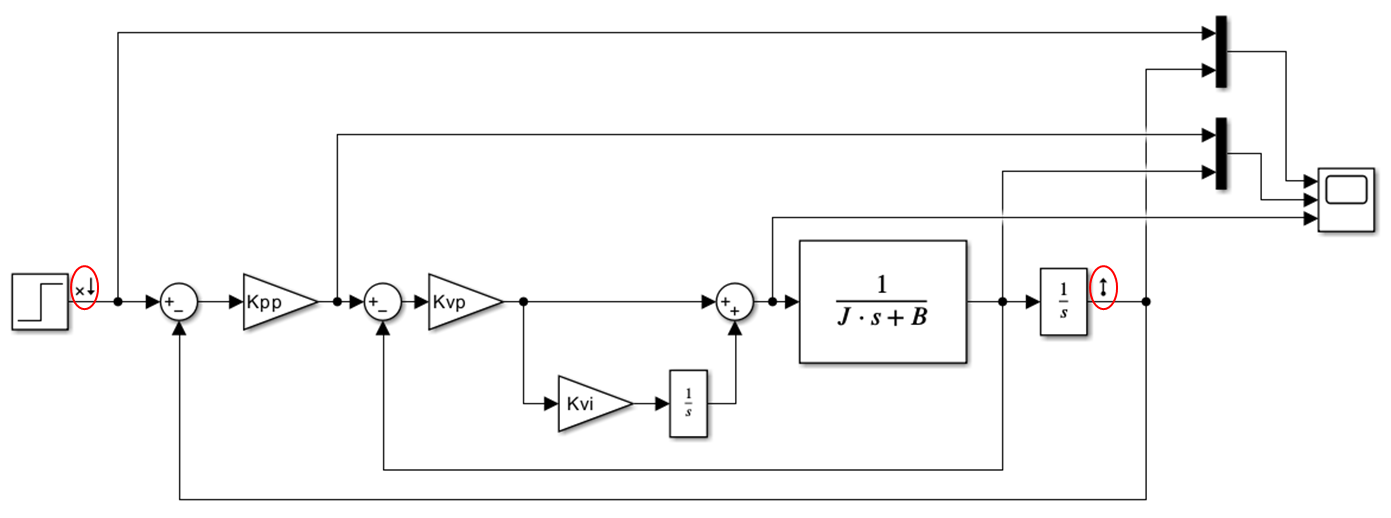
아래 결과에선 편의상 속도 지령이 사다리꼴이 되도록 위치 지령을 생성한다.

참고로, 등속구간에서 토크는 0.1Nm인데 이는 회전자 시정수, 관성모멘트, 현재 속도와 관련있다.

토크 = (관성 모멘트)/(회전자 시정수)*(현재 속도)이기 때문이다.

<그림 2. 시뮬레이션 파형>

 

 

1. 적분시정수 IT 조정

그림 2를 통해 적분시정수 IT를 조정한 결과를 비교해본다.

적분시정수 IT는 (a)와 (b)에서 각각 10, 100으로 설정했다.

<그림 3. 적분시정수 조정>

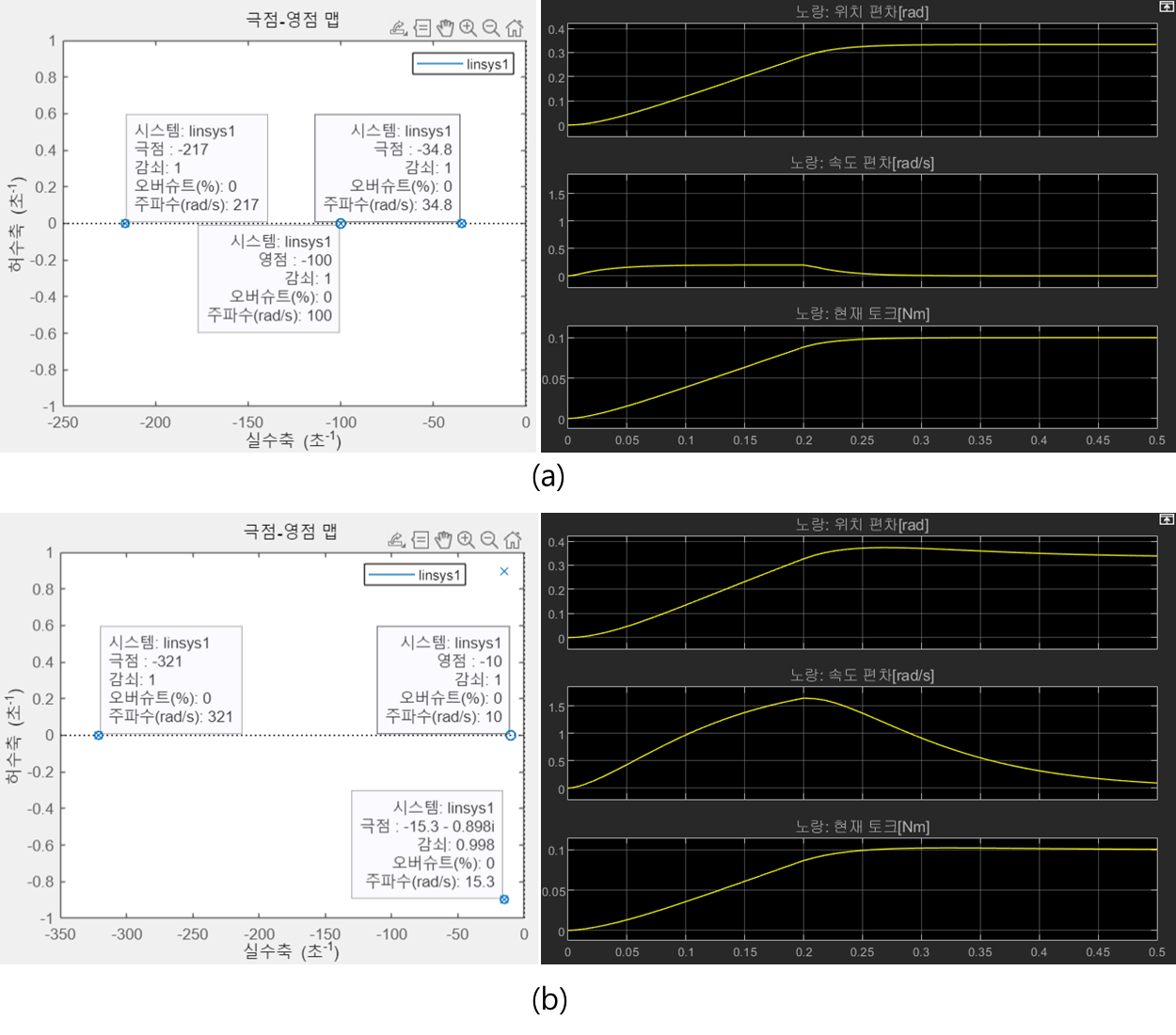
두 그래프를 분석해보자.

편의상 (a)를 기준으로 극점 -34.8, -100, -217을 각각 극점 1, 2, 3으로 부른다.

1) 극점 3은 -217에서 -321으로 이동했다.

2) 극점 1, 2는 각각 -15.3±0.898i가 되었으며, 허수부가 생겼고 원점과 더욱 가까워졌다.

3) 영점은 -100에서 -10으로 이동했다.

 

정리하면, 다음과 같다.

1) 극점 3은 원점으로부터 더욱 멀어졌으나, 극점 1과 2가 원점과 가까워짐으로써 시스템 응답이 느려졌다.

    ▶ 속도편차가 커졌으므로, 속도 추종이 느려졌다.

2) 위치 편차가 일정 값으로 수렴하는데 걸리는 시간이 오래 걸리며, 오버슈트가 생겼다.

    ▶ 극점에 허수부가 생김으로써 시스템이 조금 불안해졌다.

 

이전 포스팅에서 언급했듯이 적분시정수를 통해 "극점-영점 상쇄"를 하려면, 점성마찰계수 B를 정확하게 알고 있어야 한다.

하지만, 기계적인 특성(윤활유, 마찰, 마모 등)에 따라 같은 시스템이라도 다른 값을 가지게 된다.

따라서, 적정한 조정 범위 내에서 원하는 특성을 만족하는 값을 찾아서 적용해야 한다.

 

2. 속도 비례 게인 Kvp 조정

보통 모터드라이버 제조사의 파라미터를 보면, 편의상 속도제어기의 차단주파수 Fc[Hz]를 조정한다.

이번에는 차단주파수 Fc를 40에서 80으로 바꿔보자.

 

 

<그림 4. 속도제어기의 차단주파수 조정>

두 그래프를 분석해보자.
편의상 (a)를 기준으로 극점 -34.8, -100, -217을 각각 극점 1, 2, 3으로 부른다.

1) 극점 3은 -217에서 -471으로 이동했다.

2) 극점 1은 -34.8에서 -32로 조금 이동했다.

3) 극점 2와 영점은 위치가 동일하다.

정리하면, 다음과 같다.

1) 극점 3은 원점으로부터 더욱 멀어짐으로써 시스템의 응답이 빨라졌으나, 0.3초 이후로 속도 편차에 리플이 있다.

    ▶ 속도편차가 절반 정도로 줄어들었으나, 시스템이 조금 불안정해졌다.

2) 위치 편차의 파형은 비슷하다.

 

속도제어기의 차단주파수 Fc를 높이면, 가속하는 동안에 속도 편차가 줄어드는 효과가 있다.

하지만, 너무 빠른 응답은 오히려 시스템을 불안정하게 만든다.

하지만, 시스템이 불안정해질 수 있음에 유의해야 한다.

 

 

3. 위치 비례 게인 Kpp 조정

위치 비례 게인 Kpp를 조정할 때는 위치 편차에 주목한다.

<그림 5. 위치 비례 게인의 조정>

 

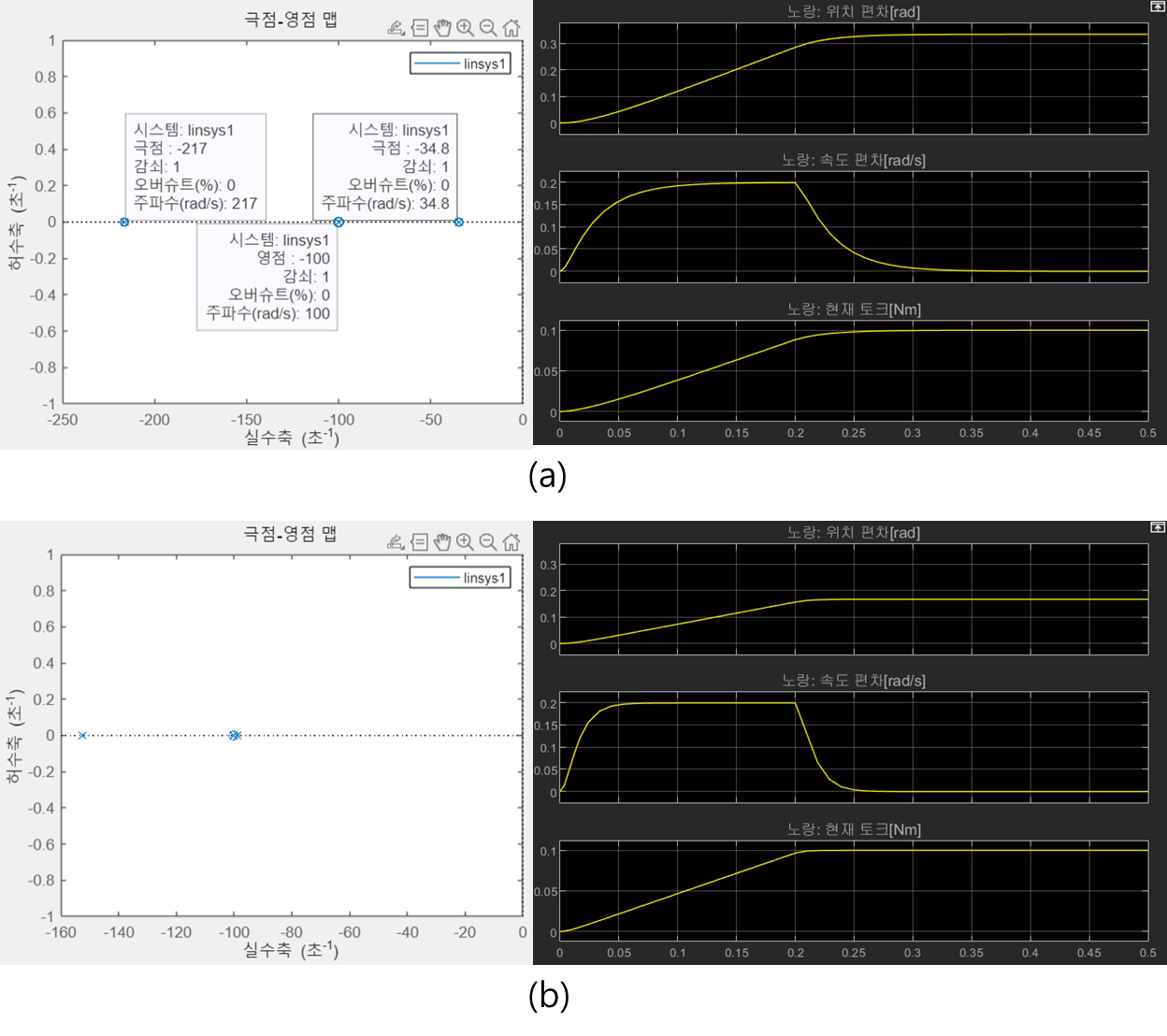
두 그래프를 분석해보자.
편의상 (a)를 기준으로 극점 -34.8, -100, -217을 각각 극점 1, 2, 3으로 부른다.

1) 극점 3은 -217에서 -156으로 이동했다.

2) 극점 1은 -34.8에서 -99로 이동했다.

3) 극점 2와 영점은 위치가 동일하다.

 

위치 비례 게인 Kpp를 120까지 올려보니 극점에 허수부가 발견되었다.

 

<그림 5. Kpp = 120일 때>

정리하면, 다음과 같다.

1) 극점 1이 원점과 멀어짐으로써 시스템의 응답이 빨라졌다.

    ▶ 위치편차가 절반 정도로 줄어들었다.

2) 위치 편차가 줄어들었기에 속도와 토크 응답 속도가 달라졌다.

3) 위치 게인을 조정하면 극점에 허수부가 생기기도 한다.

 

속도제어기의 차단주파수 Fc를 조정해도 극점이 허수부를 가지지 않을까?
결론을 말하자면, 그렇다.
다만, 일반적으로는 "위치비례게인 Kpp << 2π×(속도제어기의 차단주파수 Fc)"로 조정하기 때문에, 거의 허수부가 생기지 않는다.
일부 모터의 경우 위치비례게인 Kpp를 극단적으로 높여서 사용하는 경우가 있는데, 이 때는 극점이 허수부를 가질 수도 있다.

 

 

파라미터를 정확하게 모르는 경우엔?

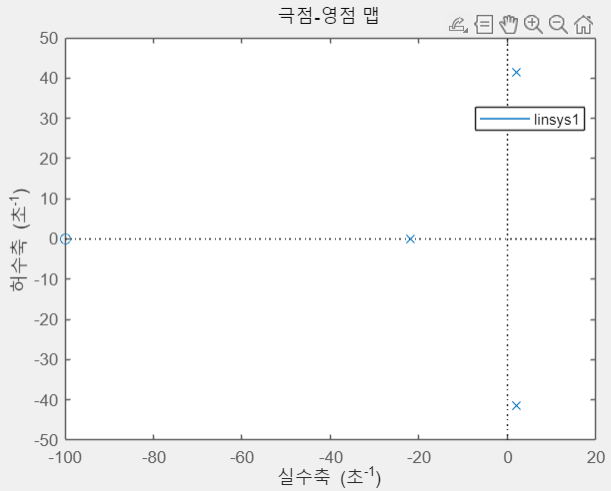
만약 모터에 매우 큰 부하가 연결되었지만, 관성비 IR을 0으로 입력해주면 어떻게 될까?

그림 6을 보면 속도와 토크 파형이 흔들리면서 불안정한 것을 볼 수 있다.

그림 7에선 극점이 우방면에 있는 걸 보아하니, 실제로 불안정해진 것이다.
보통은 조금 다른 값이 입력되었다고 크게 불안정해지진 않을 것이다.

파라미터 입력을 제대로 안 해주면 초기 기동이 불안정해서 주변에 악영향을 줄 수 있기에 항상 유의하자.

<그림 6. 모터 파라미터를 정확하게 모르는 경우>

 

<그림 7. 불안정해진 시스템>

 

 

마무리

일반적으로 모터를 제어하는 데 있어 이러한 이론을 심도있게 다루지는 않는 듯 하다.

(자동차업계나 정밀한 공정이 필요한 곳은 필요할지도...)

각각의 게인을 조정하면 어떻게 모터의 응답이 바뀌는지, 왜 모터 파라미터를 정확히 알고 있어야 하는지.

이 두 가지만 알면 왠만한 문제는 다 해결할 수 있을 것이다.