고정 헤더 영역
상세 컨텐츠
본문
현대제어 1부
고전제어 2부고전제어 1부... 현대제어와의 차이제어기 설계에 필요한 제어 이론에는 고전제어와 현대제어가 있다. 고전제어에서는 시스템을 단일 입력과 단일 출력의 전달함수로 나타낸다.그
zin9.tistory.com
이번에는 글이 조금 길 것이므로 미리 구성을 설명한다.
1. 비례게인 L 계산
2. 관측기의 물리적 이해
3. 관측기의 게인 설정
1. 비례게인 L 계산
루엔버거 관측기의 행렬식을 세우면 다음과 같다.
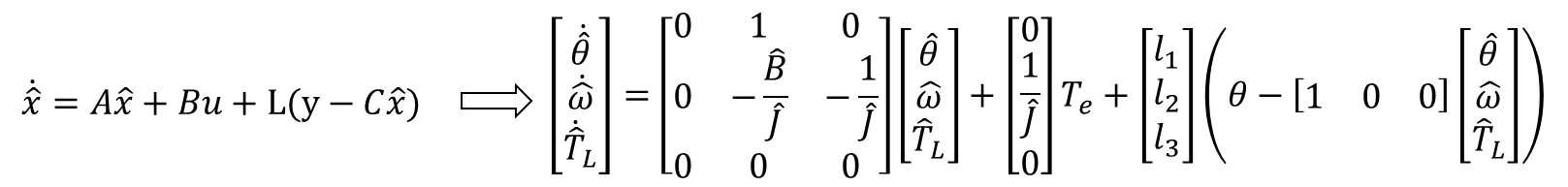
이 식을 그림으로 나타내면 다음과 같다.

행렬식을 정리하면 아래와 같이 되고, G1과 w의 항이 추가된다(외란과 관련된 항이다)
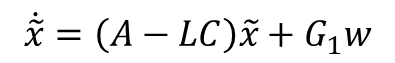
오차 관련 항인 G1w의 영향을 작게 하기 위해 아래와 같은 특성 방정식이 0이 되도록 하는 근이 3개가 나온다.
특성 방정식은 3차이므로 3x3 행렬의 고유값을 구하면 다음과 같다.
계산 과정은 생략하니 직접 해봐도 좋다.

특성 방정식의 근의 값은 속도 제어기의 대역폭의 3~5배정도로 충분히 높게 설정해야 한다.
β값이 너무 작으면 값의 수렴속도가 느려진다.
반대로 너무 크면 측정상의 잡음 또는 모델링 오차가 발생하거나 관측기가 불안정해질 수 있다.
특성 방정식의 근을 3중근으로 하면 계산이나 조정 과정이 간단해진다.
시뮬레이션에 사용한 관측기는 다음과 같다.
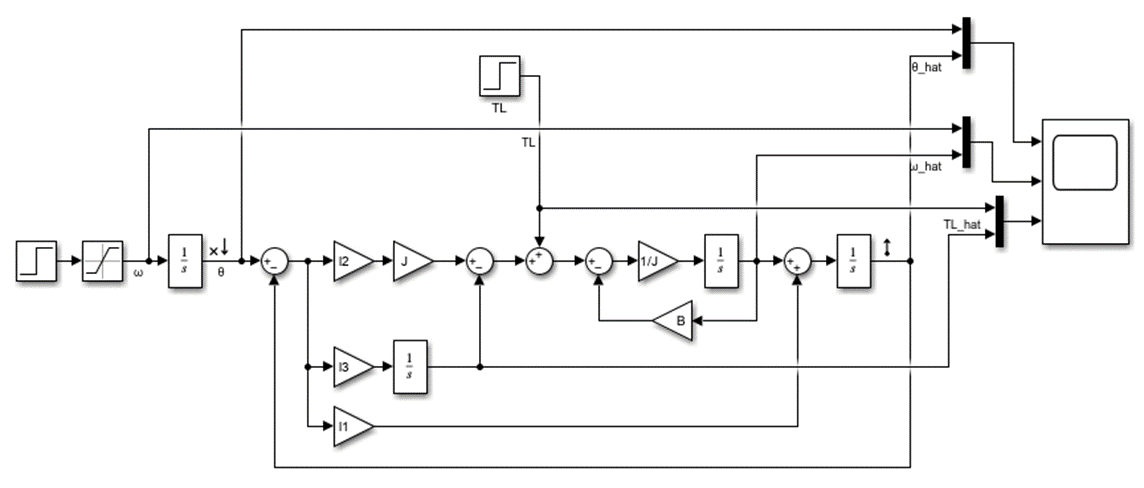
관측기를 설계해서 서로 다른 3개의 근으로 할 때와 3중근으로 할 때의 차이를 알아보자.
1) 3중근으로 한 경우
좌측은 3중근을 -100Hz로 둔 것이고, 우측은 3중근을 -200Hz으로 둔 것이다.
3중근의 값이 클수록(=s-평면에서 원점으로부터 왼쪽으로 멀어지므로) 속도를 빠르게 추종함을 알 수 있다.
(그림 2에서는 속도지령이 ramp지만, 편의상 step으로 바꿔서 파형을 비교한다.)
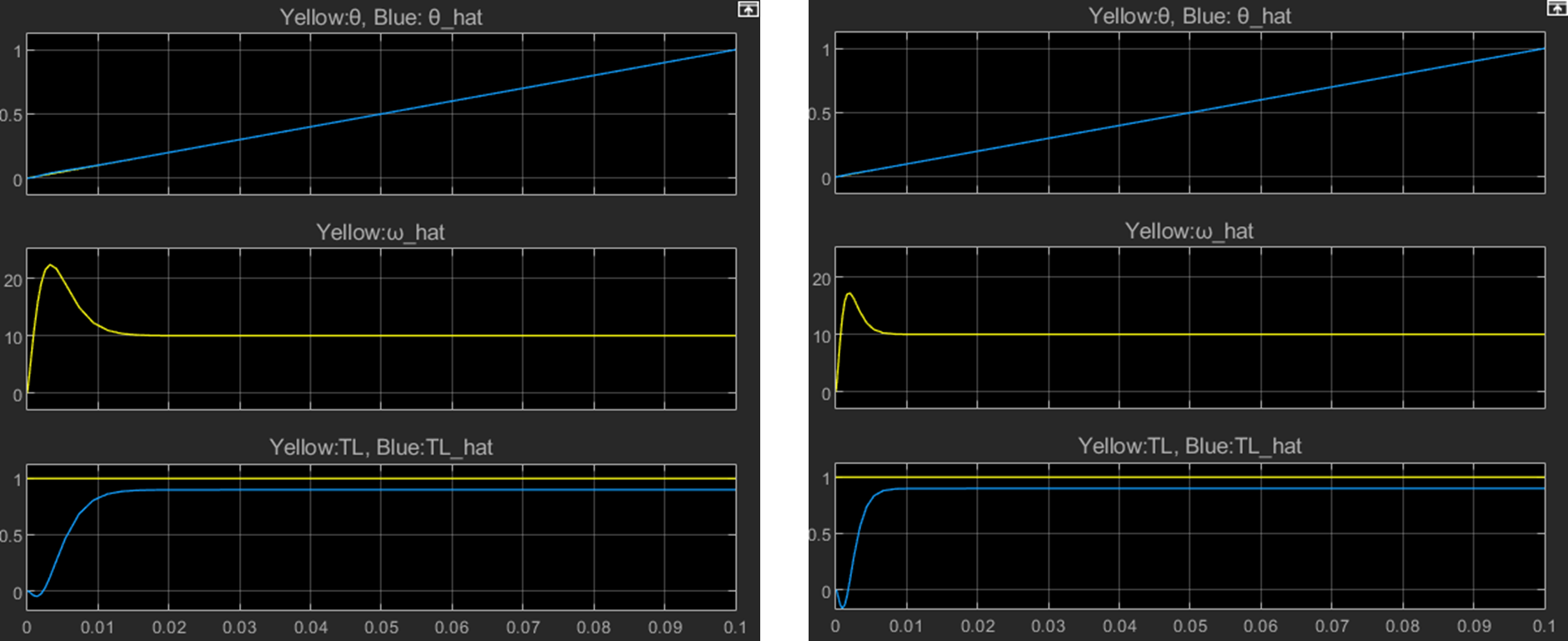
2) 서로 다른 근을 가진 경우
좌측은 3중근을 -100Hz로 둔 것이고, 우측은 각각 -400Hz, -100Hz, -100Hz으로 둔 것이다.
어떻게 조정하는 게 좋은지는 필자도 아직 잘 모르기에, 편의상 3중근으로 조정해놓고 사용하자.

※ 시뮬레이션 분석
①속도 10rad/s, B=0.01이므로 점성마찰토크는 0.1이다.
②추정 부하 토크 TL_hat은 1이 아닌 0.9(=1-0.1)으로 나타난다.
→ 부하토크에 점성마찰토크 만큼의 오차가 존재한다.
→ 점성마찰계수가 크고 속도가 빠른 시스템에서는 오차가 더욱 커진다.
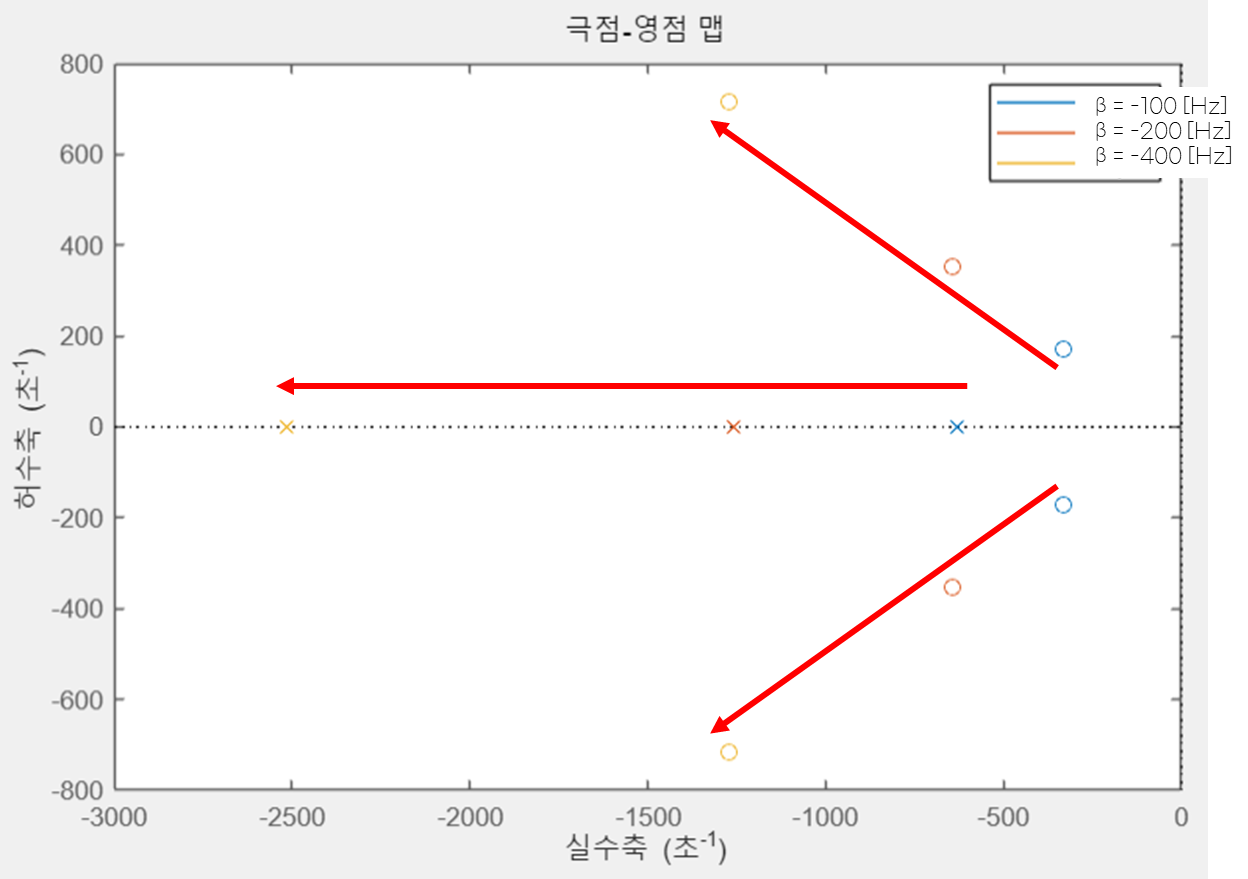
β1, β2, β3 값에 따른 근의 위치를 살펴보자.
예상하다시피 값이 커질수록 좌반면으로 이동하는 경향이 있다.
이 때, 영점은 허수부의 값이 점점 커지므로 시스템이 불안정하게 될 수도 있다.
또는 아래에서 소개하는 전달함수의 크기를 구함으로써 계산할 수도 있다.
맨 아래의 '3. 관측기의 게인 설정'의 맨 아래에서 설명하도록 한다.
2. 관측기의 물리적인 이해
그림 1의 관측기를 그림 6과 같이 나타내면 마치 PID 제어기의 형태로 볼 수 있다.
그림 6 (a)은 기존 관측기 형태이고 마치 PI 제어기와 같다.
그림 6 (b)는 l1의 위치를 바꿔서 PID 제어기 형태로 만든 것이다.
따라서, 기존의 PID 제어기와 유사하게 게인값을 조정할 수 있다.
교재에서는 그림 6 (a)의 형태로 해석하는데, 추정 속도의 기준을 2가지로 다르게 설정할 수 있기 때문이다.
(그림 8에서 추정 속도의 위치를 조정하기 위함이므로 천천히 알아보자.)

다시 나타내면 그림 7이 된다.
K1, K2, K3를 각각 미분게인, 비례게인, 적분게인으로 하여 관측기의 성능을 조절할 수 있다.

그림 7에서 측정각에 대한 추정각을 전달함수를 구하면 다음과 같다.
낮은 주파수 영역에서는 전달함수의 크기가 1이 된다.
이는 추정한 기계계의 제정수 J와 B 값이 실제값과 다르더라도 추정각이 측정각과 거의 동일함을 의미한다.
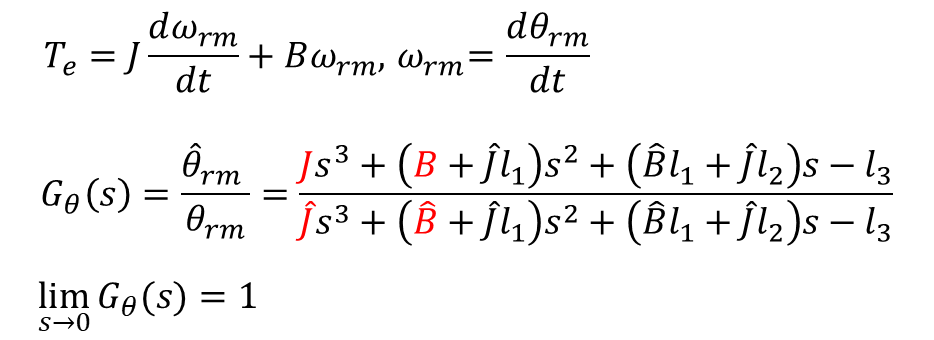
또한, 추정한 J와 l1의 곱이 B보다 크게 설정한 경우, 높은 주파수 영역에서만 전달함수가 1이 아니게 된다.
즉, 낮은 주파수 영역에서는 전달함수의 크기가 거의 1이 되어 추정각이 측정각과 거의 유사하게 됨을 알 수 있다.
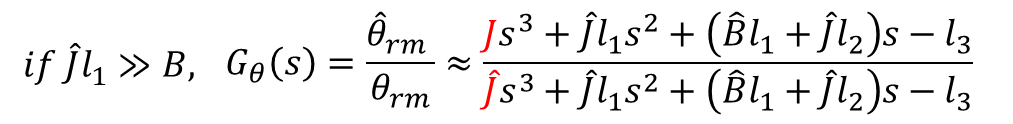
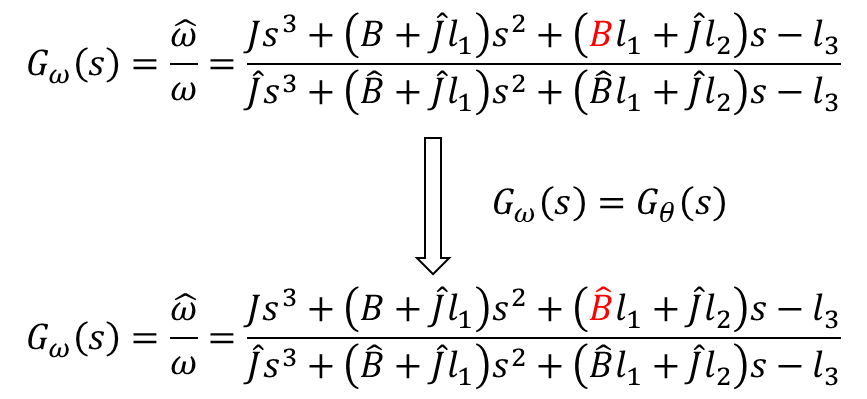
측정속도와 추정속도에 대한 전달함수도 아래와 같이 구할 수 있다.위에서 구한 '측정각과 추정각에 대한 전달함수'와 동일하게 하기 위해 그림 8와 같이 바꾸보자.이로써 '측정각과 추정각에 대한 전달함수' = '측정속도와 추정속도에 대한 전달함수'가 된다.
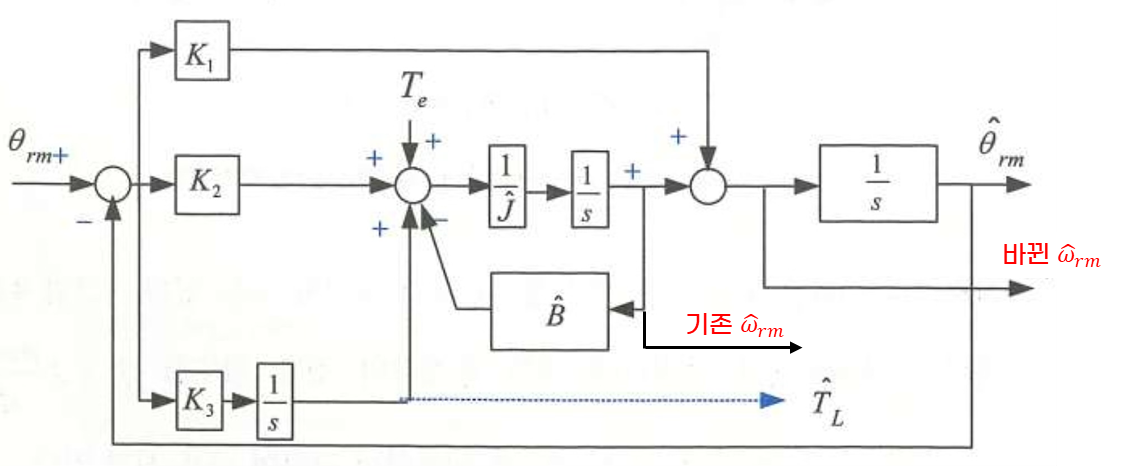
이번에도 '낮은 주파수 영역'에서는 제정수 오차에 강인한 속도 추정이 가능하다.다만, K1이 포함된 측정 오차가 속도 추정치에 영향을 주므로, 추정된 속도가 위치 측정 잡음에 민감해지는 단점이 있다.
3. 관측기의 게인 설정
θrm을 생성하는 순서이다.
1) 원하는 관측기의 대역폭의 10% 정도의 주파수로 설정한다.
→ 원하는 대역폭을 50[Hz]으로 가정한다.
2) 구형파의 크기는 측정 범위를 벗어나지 않도록 지속적으로 조정한다.
→ 구형파의 진폭은 0부터 10[rad]으로 한다.
조정 순서
순서 1) 모든 게인 및 Te를 0으로 한다.
순서 2) 약 10% 내외의 오버슈트가 생길 때까지 비례 게인 K2를 증가시킨다.
순서 3) K2를 고정시키고, 대부분의 오버슈트가 없어지도록 미분 게인 K1를 증가시킨다.
순서 4) K2과 K1을 고정시키고, 약 10% 내외의 오버슈트가 생기도록 적분 게인 K3을 증가시킨다.
순서 5) 입력을 제어 대상 시스템에서 받고, 전향 보상항 Te도 제어기 출력에서 받는다.
순서 6) 실제 운전 상황에서 관측기의 입력/출력 특성을 보아가며 게인 값을 미세조정한다.
자, 시뮬레이션으로 해보자.
대역폭을 더 높여서 해보고 싶지만, PWM 생성에서 5Hz정도로 해야만 오버슈트를 볼 수 있다.
순서 2) K2 = 0.8으로 하면 오버슈트가 약 10%정도 생긴다.
순서 3) K1 = 500으로 하면 오버슈트가 거의 없어진다.
순서 4) K3 = 500으로 하면 오버슈트가 약 10% 정도로 생긴다.

순서 5) 구성된 시뮬레이션 블록은 다음과 같다.
0.5초에 0.1Nm의 외란 토크가 step 응답의 형태로 입력된 상황을 가정한다.

순서 6) 외란토크가 입력되었으나, 실제 속도값(파랑)과 추정 속도값(주황)은 동일하게 나타난다.(그림 11에서는 실제 속도값(파랑)이 추정 속도값(주황)와 동일하므로 가려졌다.)

이로써 관측기의 성능 검증까지 완료되었다.
※ 비례 게인 L의 계산 방법
위의 시뮬레이션에서 K1, K2, K3은 각각 500, 0.8, 500이다.
그림 10에서 사용한 모터의 관성모멘트 J는 0.0001이다.
따라서, l1 = 500, l2 = 8000, l3 = -500이 된다.
그렇다면 역으로 β1, β2, β3을 구할 수 있다.
따라서, β1 = -100, β2 = -250 - 50√5, β3 = -250 + 50√5 가 된다.
추가)
루트가 보기 불편하므로, β2와 β3를 -200인 2중근으로 해보자.
(2차 방정식이 s²+500s+50000=0이므로)
그렇다면 l1 = 400, l2 = 40000, l3 = -400이 된다.
이것을 게인으로 변환하면, K1 = 400, K2 = 4, K3 = 400이 된다.
비례게인이 다소 커졌으나, 그 결과는 그림 11과 거의 똑같다.
다만 3개의 근에 허수부가 없다는 장점이 생겼다.
어느정도의 허수부가 불편하다면 이렇게 반복작업을 통해 없앨 수 있을 것이다.
작은 허수부는 시스템의 안정성에 영향을 미치진 않겠지만...
이상 길었던 속도 관측기 설계를 마친다.다음 시간에는 외란관측기에 대해 알아본다.
출처: 전기기기제어론 4.3.3 상태 관측기를 이용한 속도의 추정
'제어이론' 카테고리의 다른 글
| 현대제어 1부 - 관측기의 이해 (1) | 2024.06.10 |
|---|---|
| 고전제어 1부... 현대제어와의 차이 (0) | 2024.06.09 |
| 약계자 제어(Field Weekening Control) - 1부 (3) | 2024.03.30 |
| PWM 이해하기 - 2부 (5) | 2024.02.19 |
| PWM 이해하기 (2) | 2024.01.29 |




